Eukaryode: Tectonic Interpolation
Recently I’ve started work on a game. I want to make a tile-based ecology sim covering the history of multicellular life on Earth. For now, I’m naming it Eukaryode.
I’m creating this game in the Monogame framework, a C# framework on which Unity3D is based. This was motivated by my desire to get out of Unity, and into something more elementry, giving me the chance to build more performant systems and manageable content pipelines.
I haven’t added any animals or plants to Eukaryode, yet. That’s because there’s an important feature I want to prototype first: plate tectonics.
A Little History of Plate Tectonics
The shifting of Earth’s continents over millions of years is common knowledge. 500 million years ago, during the Ediacaran period when I hope to start the game, the continental landmasses were united mostly in the Southern Hemisphere, in a supercontinent called Pannotia. In the abundant shallow seas around this continent, we think the first complex multicellular animals appeared.
300 mya, in the Permian, Pannotia has briefly fragmented only to reunite as the more famous Pangaea. Since not much rainfall can make it to the interior of this huge landmass before precipitating, the Permian is characterised by desertification, and it’s this climate that pressures the evolution of animals with hard-shelled eggs - reptiles and stem-mammals - to outcompete the planet’s giant amphibians.
At 64mya, the immediate aftermath of the asteroid that wiped out the dinosaurs, the familiar world map is taking shape. South America, Antarctica, and Australia were until recently united, and insulate a unique variety of marsupials which today survive as Kangaroos, Koalas, and Opossums. India moves rapidly to Asia where its collision will raise the Himalayas - all while whales evolve on the shores of Pakistan. The joining of North and South American will see the Great American Biota Exchange, in which Northern species generally outcompete those in the South, while the Berring Land Bridge will facilitate the colonisation of Eurasia by horses and camels, and the Americas by humans.
I want a game about the history of life on Earth to feature its dynamic geography, where continental changes can dry rainforests, raise sea levels, and exchange species.
Tectonic Interpolation
Writing a true simulation of plate tectonics is too difficult for me. It would allow me to add mechanics to change the course of Earth’s history (e.g. what if India went south instead of north?), but I’m not sure that’s what I want. Instead, I want the familiarity of Earth as we know it.
The player can then respond to these changes in advance - e.g. by evolving cold-resistant animals when an ice age is on its way.
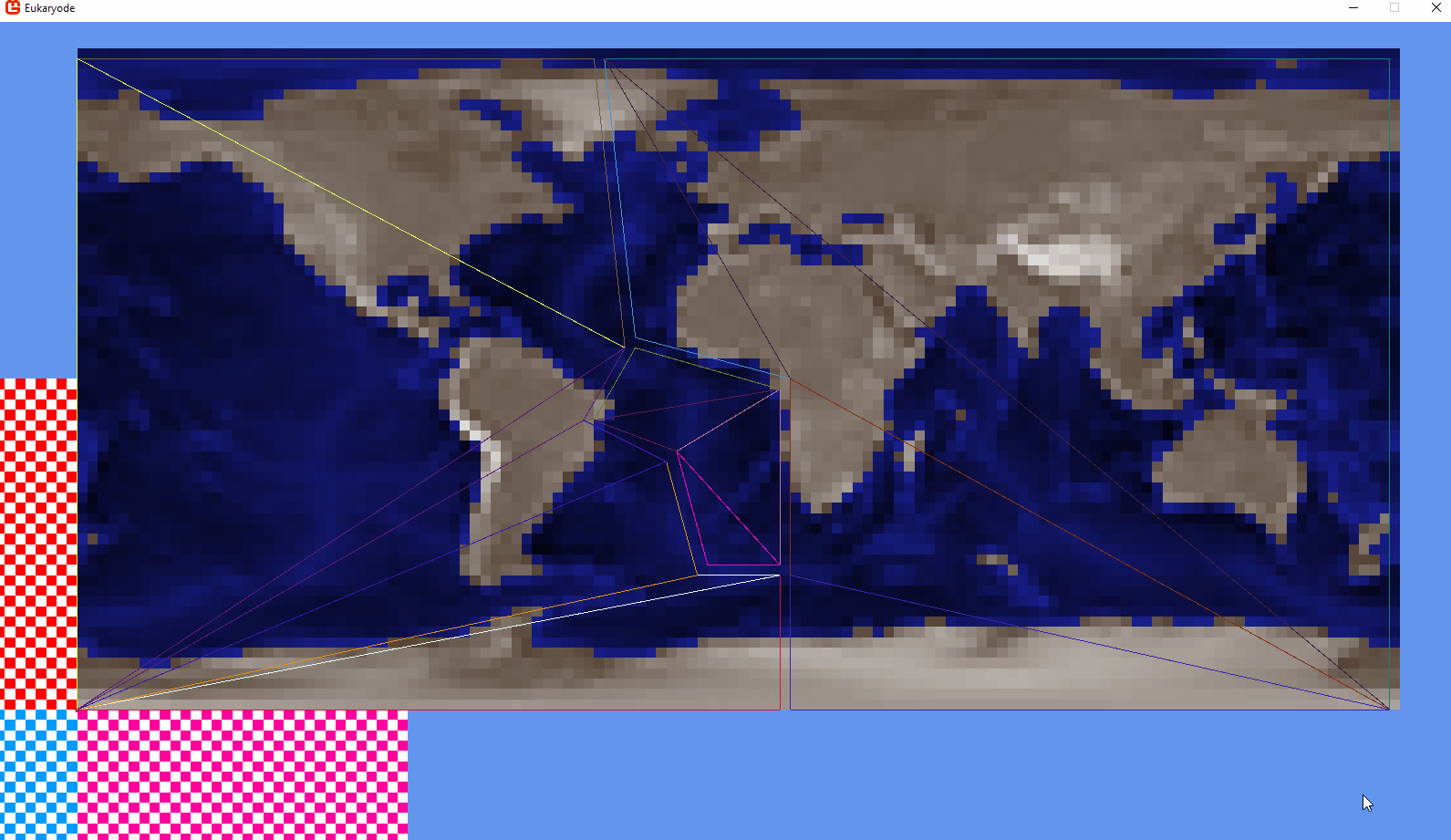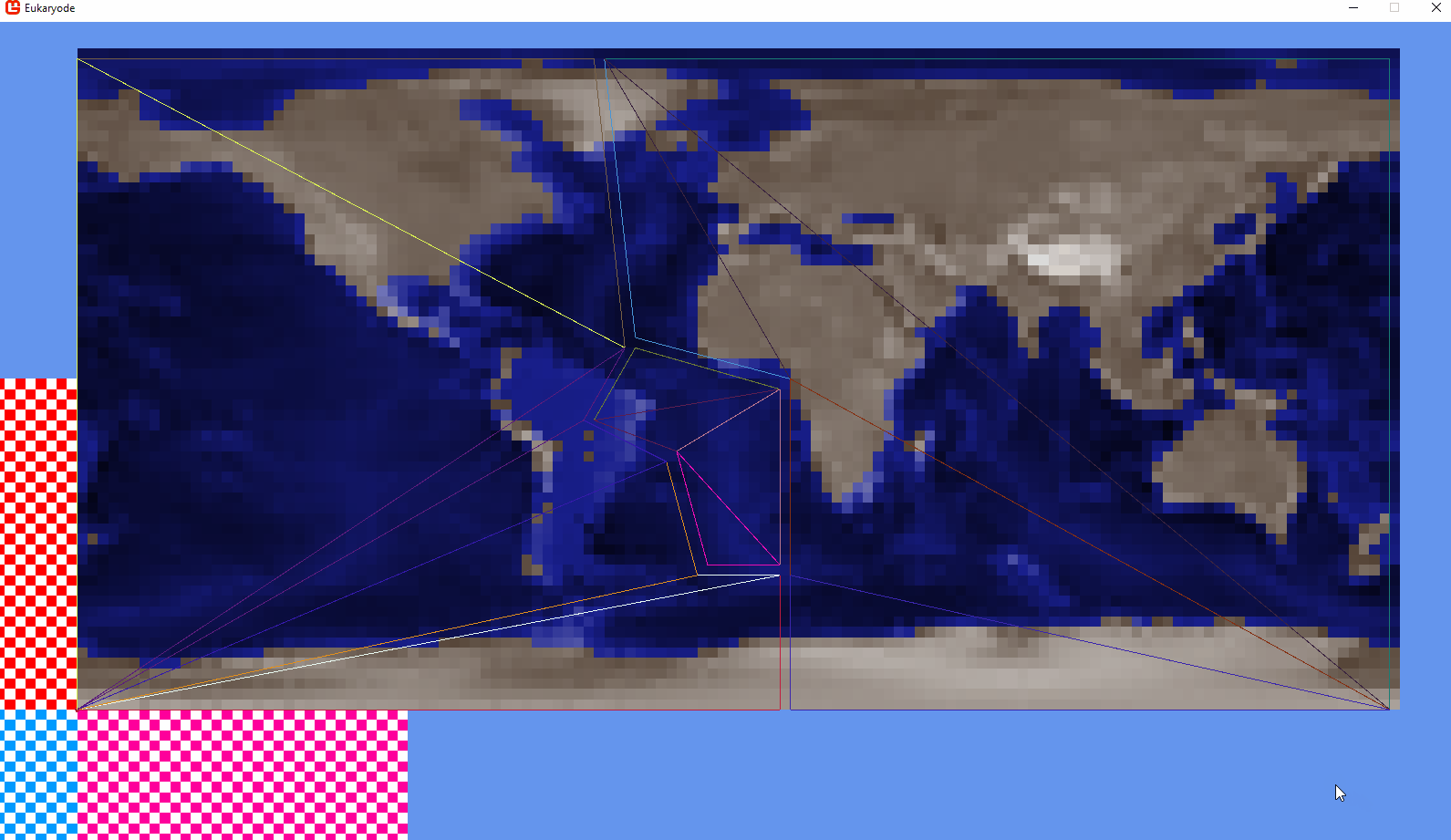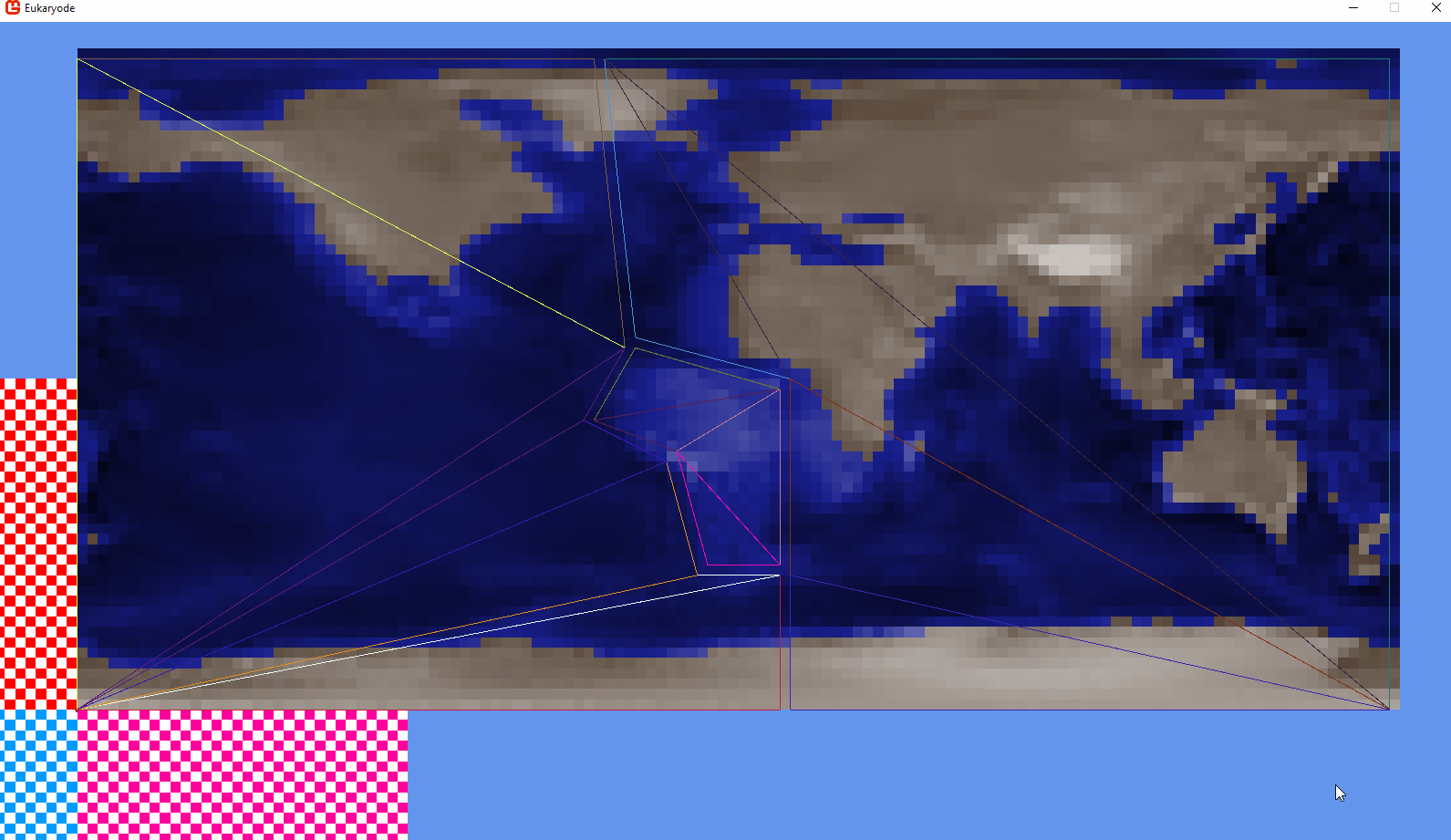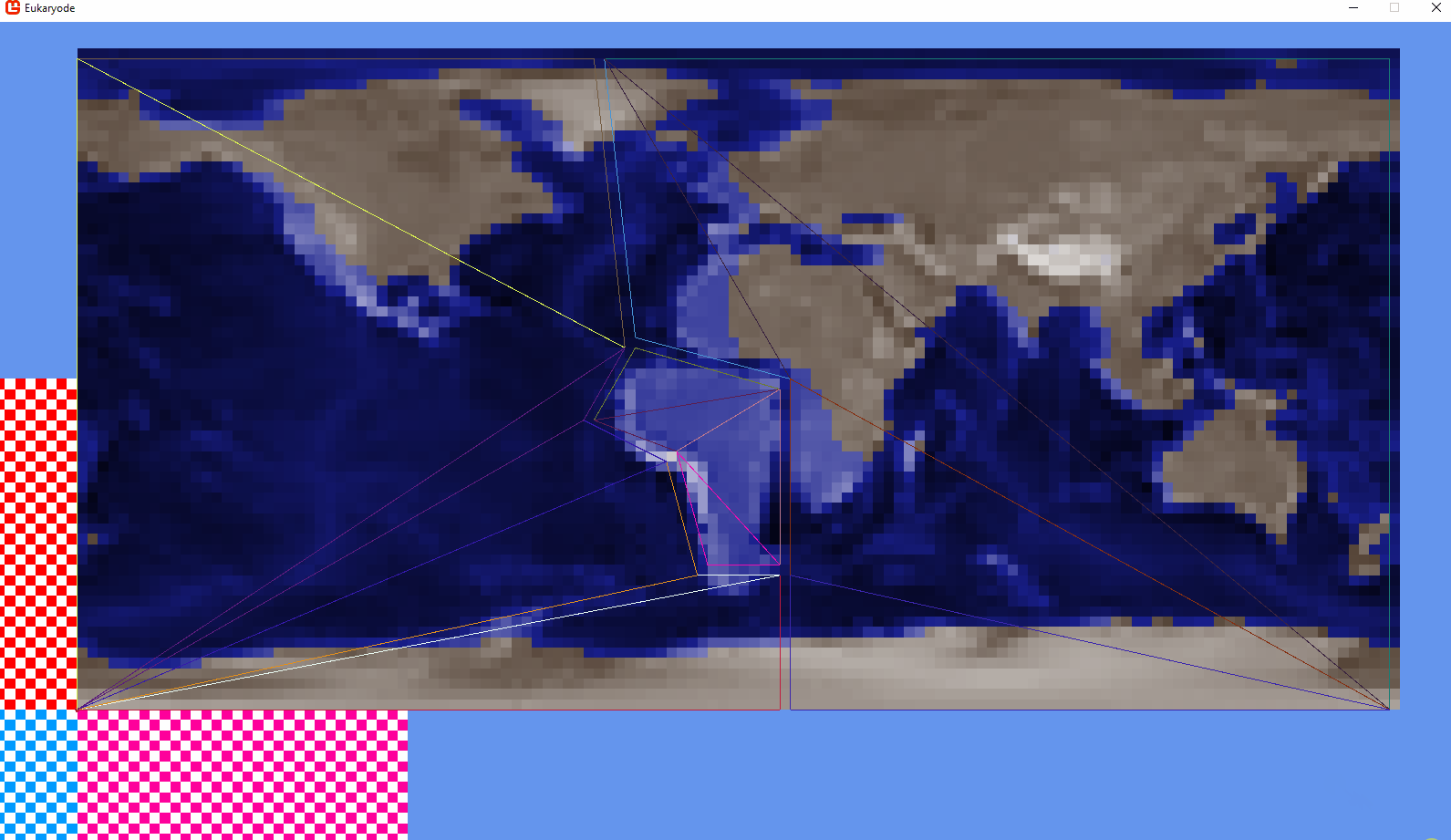
So I’m implementing a system that interpolates between fixed snapshots of the earth’s surface. For example, given these two maps, I’d want South American to gradually move towards Africa.
The system ideally needs the following properties:
The game knows where a given map tile is going, based on that map tile’s position in the first, and second snapshot.
As map tiles move, animals and plants move with them, so that South America carries its flora and fauna to North America rather than them just sliding off into the ocean.
Landmasses stay as solid as possible when they move. We want to avoid tiles becoming unexpectedly submerged, drowining anything that was sitting on them.
How It’s Done
To solve this problem, I started by scribbling a lot in my notebook. My first attempt was an algorithm like this:
For a given point P1 in an initial polygon
Take the vectors from P1 to each polygon corner
Now add each vector to their respective corners in the 2nd polygon
Take the average of these new positions to get P2
As my toy example somewhat demonstrates, this did not work.
Barycentric Coordinates
After asking some programmer friends, I was introduced to Barycentric Coordinates. This is a Vector 3 that describes a point within a given triangle (it specifies the weighting or ‘mass’ of each corner of the triangle, such that if we threw the triangle into the air, it would rotate on our point).
If I obtain the barycentric coordinate of a point in one triangle, and apply it to another triangle, I get that same point’s analogue in the 2nd triangle. So for a tile in snapshot A, I can determine where it’s going in snapshot B.
See the code for converting to and from barycentric coordinates below:
/// <summary>
/// Convert a cartesian point to its barycentric coordinate relative to a triangle.
/// The triangle's points must be in counter-clockwise order.
/// </summary>
/// <returns>
/// Returns a Vector 3 coordinate where:
/// X is the mass of triA,
/// Y is the mass of triB,
/// Z is the mass of triC.
/// </returns>
public static Vector3 CartesianToBarycentric(Vector2 triA, Vector2 triB, Vector2 triC, Vector2 cartesian)
{
float triArea = GetTriangleArea(triA, triB, triC);
if(triArea < 0f)
{
throw new ArgumentException($"Triangle area was found to be a negative number. The triangle points provided must be in counter-clockwise order.");
}
float w = GetTriangleArea(triA, triB, cartesian);
float v = GetTriangleArea(triA, cartesian, triC);
float u = triArea - (w + v);
float normalizeFactor = 1f / triArea;
return new Vector3(u, v, w) * normalizeFactor;
}
/// <summary>
/// Convert a barycentric coordinate relative to a triangle to the cartesian point it represents.
/// The triangle's points must be in counter-clockwise order.
/// </summary>
public static Vector2 BarycentricToCartesian(Vector2 triA, Vector2 triB, Vector2 triC, Vector3 barycentric)
{
return barycentric.X * triA + barycentric.Y * triB + barycentric.Z * triC;
}
Ear-Clipping Triangulation
Where are these triangles coming from? All I’ve shown so far are two heightmaps, one with South America next to Africa.
My plan was initially to define polygons on each snapshot map, using an index image:
The background colours are each a plate. I’ve only got 3 for now, with South America (purple) being the one we care about.
Each dot is a unique colour representing a polygon’s vertex.
I then use a json file to describe which vertices and which background colour signifies which tectonic plate.
(For the curious, all my Jsons are loaded into the game using an extended JsonContentTypeReader, which is provided by the very helpful Monogame.Extended library. This post covers how to use it.)
{
"Plates": [
{
"Name": "SouthAmericanPlate",
"KeyColor": "40, 0, 40",
"Vertices": [
"137, 158, 255",
"255, 253, 107",
"255, 161, 8",
"100, 137, 0",
"0, 64, 0",
"0, 38, 97"
]
},
{
"Name": "RightPlate",
"KeyColor": "0, 40, 0",
"Vertices": [
"255, 174, 97",
"227, 255, 129",
"64, 255, 238",
"0, 252, 35",
"72, 110, 255",
"191, 32, 255",
"223, 0, 0"
]
},
{
"Name": "LeftPlate",
"KeyColor": "0, 0, 40",
"Vertices": [
"212, 174, 0",
"32, 255, 252",
"104, 0, 140",
"0, 4, 244",
"250, 0, 23",
"213, 0, 247",
"255, 232, 102",
"255, 61, 38",
"40, 220, 0"
]
}
]
}
We’ve defined polygons, but barycentric coordinates need triangles.
I’m able to automatically break down polygons into triangles using Ear Clipping Triangulation. It works by:
Finding an ‘ear’ vertex (a vertex with an internal angle < 180 degrees, and, when you make a triangle with it and its left and right neighbor, it contains no other vertices)
2. Declaring that vertex and its neighbors a triangle and ‘cutting it off’ from the remaining polygon, then repeating the process.
This lets me reliably split each tectonic snapshot into triangles. Then, for each tile in the first snapshot, I find what triangle it’s in, find where that triangle has moved in the next snapshot, and convert the barycentric coordinate back to cartesian coordinates to get the tile’s target position.
(The source code for my Ear Clipping algorithm will be at the end of the post)
Tectonic Flow Algorithm
All this gets me a big array of tiles which know where they want to move in order to match the target snapshot.
But how do we actually move these tiles, frame by frame? Remember, we want to try and preserve landmasses, all while moving the animals and plants on the tiles.
Moving points around a grid in a flowy way sounds a lot like fluid dynamics and vector fields: there’s lots of established math behind this, but I’ve tried learning about it before and it’s a bit too much for me.
So I tried putting something together by myself. After a lot of notebook scribbling, I settled on this algorithm:
We have a grid of cells, representing the game map.
Each cell has an occupant. The occupant is a ‘point’. While a cell is always at an integer coordinate (e.g. [1, 1]), the occupant can be at a continuous coordinate, and move gradually between cells (e.g. [1.78, 0.62]).
Occupant Points move from their origin on the first snapshot, to their destination on the second, as determined by our barycentric method.
When an Occupant Point crosses over from one cell to another, it becomes an incoming occupant of that cell: it wants to occupy the new cell on the next tick.
At the end of each tick, every cell needs to have exactly one Occupant. But some Occupants have left their original cell, and some cells now have multiple Occupants wantint to occupy them. So we do Merge, Move, and Split commands on each cell to get things back to one-occupant-per-cell.
Finally, interpolate altitudes towards the target heightmap.
There are still issues with this algorithm, but fixing them will take time.
An outline of the 3 commands that can be generated by stage 5 of the algorithm:
Here’s an earlier pass of this algorithm which, due to a mistake in how I was getting the target altitude, was submerging South America.
And here’s the current version:
Some takeaways:
South America is pretty well behaved, being the smaller plate.
You can see that most of Africa gets submerged, only to reform from tiles which were originally in the Indian Ocean. This is due to my reliance on barycentric coordinates, but it’s not clear if it’ll go away as I break the map into more triangles (it probably won’t). To solve it, I’m trying to figure out a way of specifying which side of the plate generates new tiles (i.e. which side is a 'divergent border’, such as the atlantic rift).
Generally, defining plate polygons and vertices on those index-maps is really hard, and I made numerous mistakes while doing just one plate. For this reason, I’m currently implementing ImGui into my project so that I can build a simple map editor.
As mentioned, below is the full code for my Ear Clipper algorithm (I might be missing a few of the utility methods, in which case, sorry!):
using Microsoft.Xna.Framework;
using System;
using System.Collections.Generic;
using System.Linq;
namespace Amino
{
/// <summary>
/// Takes a simple, non-self-intersecting polygon defined by a list of positions counter-clockwise positions, and determines its triangles.
/// </summary>
public class EarClipper
{
/// <summary>
/// The vertices defining the polygon to be triangulated. This does not change as the algorithm executes.
/// Indices in <see cref="_clippedPolygon"/> and elsewhere refer to these vertices.
/// </summary>
private IList<Vector2> _originalPolygon;
/// <summary>
/// The current polygon which iteratively has its ears removed.
/// This is a list of the indicies of <see cref="_originalPolygon"/>, and thus starts as a list { 0, 1, ... _originalPolygon.Count - 1 }
/// </summary>
private LinkedList<int> _clippedPolygon;
/// <summary> How many verts are left in <see cref="_clippedPolygon"/>. </summary>
private int _remainingVertCount;
/// <summary>
/// Any verts which have been found to be 'ears'
/// (verts with a convex angle, which contain no other verts within the triangle formed by them and their neighbors).
/// </summary>
private HashSet<LinkedListNode<int>> _ears = new HashSet<LinkedListNode<int>>();
/// <summary> Any verts which have been found to have an angle of greater than 180 degrees. </summary>
private HashSet<int> _concave = new HashSet<int>();
/// <summary> The results of the triangulation. Each three elements represents a triangle, by its corner's indices in <see cref="_originalPolygon"/>. </summary>
List<int> _triangles;
/// <summary> How many triangles were expected given the initial vertex count: this is always (vertex count) - 2 * 3 </summary>
private int _expectedTriCount;
public EarClipper(IList<Vector2> polygon)
{
if(polygon.Count < 3)
{
throw new ArgumentException($"Cannot triangulate a polygon that has vertex count ('{polygon.Count}') of less than 3.");
}
_originalPolygon = polygon;
_remainingVertCount = polygon.Count;
_expectedTriCount = (polygon.Count - 2) * 3;
_triangles = new List<int>(_expectedTriCount);
Triangulate();
}
/// <summary> Run the triangulation. </summary>
private void Triangulate()
{
if (MathUtils.IsClockwise(_originalPolygon))
{
throw new ArgumentException($"The provided polygon of length ({_originalPolygon.Count}) was found to have a mostly external area, indicating that it's vertices are not counter-clockwise or that it is self-intersecting. Only simple polygons (non-self-intersecting) can be Ear Clipped, and their vertices should be in counter-clockwise order.");
}
if (_originalPolygon.Count() == 3)
{
_triangles.AddRange(Enumerable.Range(0, 3));
}
_clippedPolygon = new LinkedList<int>(Enumerable.Range(0, _originalPolygon.Count()));
// Start by determining all convexes, concaves, and ears.
LinkedListNode<int> currentNode = _clippedPolygon.First;
while(currentNode != null)
{
UpdateNodeStatus(currentNode);
currentNode = currentNode.Next;
}
Clip(_ears.First());
if(_triangles.Count != _expectedTriCount)
{
throw new InvalidOperationException($"After triangulation, polygon with vertex count '{_originalPolygon.Count}' was expected to have {_expectedTriCount} registered triangle verts, but instead had '{_triangles.Count}'. This means the algorithm has not worked.");
}
}
/// <summary> Remove a given ear vertex, and recursively continue to remove ear vertices until triangulation is complete. </summary>
private void Clip(LinkedListNode<int> earNode)
{
if (!_ears.Remove(earNode))
{
throw new ArgumentException($"Cannot clip the ear with index '{earNode.Value}' because it was not within the ear set.");
}
GetNeighbors(earNode, out LinkedListNode<int> earStartNode, out LinkedListNode<int> earEndNode);
// Add the triangle in counter-clockwise order.
_triangles.Add(earStartNode.Value);
_triangles.Add(earNode.Value);
_triangles.Add(earEndNode.Value);
_clippedPolygon.Remove(earNode);
_remainingVertCount--;
UpdateNodeStatus(earStartNode);
UpdateNodeStatus(earEndNode);
if(_remainingVertCount == 3)
{
_triangles.AddRange(_clippedPolygon);
return;
}
Clip(_ears.First());
}
/// <summary> Re-evaluate if a node is concave and if it qualifies as an ear vertex. </summary>
private void UpdateNodeStatus(LinkedListNode<int> vertexNode)
{
if (IsConvex(vertexNode))
{
_concave.Remove(vertexNode.Value);
if(TriangleContainsPoints(vertexNode))
{
_ears.Remove(vertexNode);
}
else
{
_ears.Add(vertexNode);
}
}
else
{
_concave.Add(vertexNode.Value);
_ears.Remove(vertexNode);
}
}
private bool IsConvex(LinkedListNode<int> vertexNode)
{
GetNeighbors(vertexNode, out LinkedListNode<int> prevNode, out LinkedListNode<int> nextNode);
Vector2 prev = _originalPolygon[prevNode.Value];
Vector2 current = _originalPolygon[vertexNode.Value];
Vector2 next = _originalPolygon[nextNode.Value];
return MathUtils.Angle(next - current, prev - current) <= 0f;
}
/// <summary> Determine if the triangle formed by this node and its two neighbors contains any other vertices. </summary>
private bool TriangleContainsPoints(LinkedListNode<int> vertexNode)
{
GetNeighbors(vertexNode, out LinkedListNode<int> previous, out LinkedListNode<int> next);
int a = previous.Value;
int b = vertexNode.Value;
int c = next.Value;
foreach(int concave in _concave)
{
if(concave == a || concave == b || concave == c)
{
continue;
}
if (MathUtils.TriangleContainsPoint(_originalPolygon[a], _originalPolygon[b], _originalPolygon[c], _originalPolygon[concave]))
{
return true;
}
}
return false;
}
private void GetNeighbors(LinkedListNode<int> vertexNode, out LinkedListNode<int> previous, out LinkedListNode<int> next)
{
previous = vertexNode.Previous ?? vertexNode.List.Last;
next = vertexNode.Next ?? vertexNode.List.First;
}
/// <summary>
/// Get the results of this triangulation.
/// This is an array of indices, with each trio of indices being the counter-clockwise points on the original polygon that define the triangle.
/// </summary>
/// <returns></returns>
public int[] GetTriangles() => _triangles.ToArray();
/// <summary>
/// Triangulate the provided <paramref name="polygon"/> using the ear-clipping method.
/// The polygon must have no holes in it, and must not self-intersect, for the results to be accurate.
/// </summary>
public static int[] Triangulate(IList<Vector2> polygon)
{
EarClipper clipper = new EarClipper(polygon);
return clipper.GetTriangles();
}
}
}
public static class MathUtils
{
/// <summary> Determine if <paramref name="point"/> falls within the counter-clockwise triangle. </summary>
public static bool TriangleContainsPoint(Vector2 triA, Vector2 triB, Vector2 triC, Vector2 point)
{
Vector3 barycentric = CartesianToBarycentric(triA, triB, triC, point);
return barycentric.X >= 0f && barycentric.Y >= 0f && barycentric.Z >= 0f;
}
/// <summary>
/// Get the signed angle that <paramref name="v1"/> must rotate, clockwise, to align with <paramref name="v2"/> (in degrees).
/// A value greater than 180 or -180 is never returned.
/// </summary>
public static float Angle(Vector2 v1, Vector2 v2)
{
float dot = v1.Dot(v2);
float determinant = v1.X * v2.Y - v1.Y * v2.X;
return -MathHelper.ToDegrees((float)Math.Atan2(determinant, dot));
}
/// <summary>
/// Determine if the provided list of vertices run clockwise or counterclockwise.
/// This is done by determining if the enclosed area is positive or negative. For self-intersecting polygons, a 'mostly positive'
/// i.e. mostly-internal area will still be considered clockwise.
/// A shape with an area of 0 is considered clockwise.
/// </summary>
public static bool IsClockwise(IList<Vector2> polygon) => GetPolygonArea(polygon) <= 0f;
/// <summary>
/// Get the area of the specified triangle.
/// Invokes <see cref="GetPolygonArea(IList{Vector2})"/>.
/// </summary>
public static float GetTriangleArea(Vector2 a, Vector2 b, Vector2 c) => GetPolygonArea(new Vector2[] { a, b, c });
/// <summary>
/// Get the area of a polygon with no holes in it.
/// If the polygon's vertices are in clockwise order, the area will be positive, and will otherwise be negative.
/// A self-intersecting polygon's area will be the sum of all area on the right and left side of its edge,
/// so that a self-intersecting polygin that is 'mostly' clockwise will still return a positive area.
/// </summary>
public static float GetPolygonArea(IList<Vector2> polygon)
{
float sum = 0f;
for (int p = 0; p < polygon.Count; p++)
{
Vector2 current = polygon[p];
Vector2 next = polygon[(p + 1) % polygon.Count];
sum += (next.X - current.X) * (next.Y + current.Y);
}
return -sum * 0.5f;
}
}